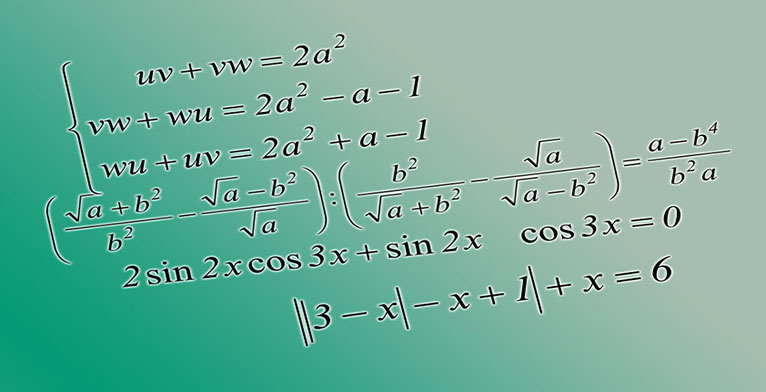При розв’язуванні задач зручно користуватися правилами суми та добутку.

Правило суми: якщо деякий об’єкт А можна вибрати m способами, а інший об’єкт В можна вибрати n способами, то вибір "Або А, або В" можна здійснити m+n способами.

При використанні правила суми потрібно слідкувати, щоб жоден із способів вибору об’єкта А не співпадав із жодним способом вибору об’єкта В.

Приклад 1.

У вазі лежать чотири яблука та три груші. Скількома способами можна обрати один фрукт?

Розв’язання.

Якщо у вазі лежать 4 яблука, то одне яблуко можна обрати чотирма способами (можемо взяти одне із 4 яблук). Якщо у вазі лежать 3 груші, то одну грушу можна обрати трьома способами (можемо взяти одну із трьох груш). А обрати один фрукт можна 4+3=7 способами.

Правило добутку: якщо деякий об’єкт А можна вибрати m способами і після кожного такого вибору інший об’єкт В можна вибрати n способами, то вибір пари (А; В) у вказаному порядку можна здійснити mn способами.

Приклад 2.

Скількома способами можна вибрати голосну та приголосну літери зі слова "приклад"?

Розв’язання.

Голосну літеру можна вибрати 2 способами (можна взяти одну з літер "а" або "и"). Приголосну літеру можна вибрати 5 способами (можна взяти одну із літер "п", "р","к", "л", "д"). Для кожного з 2 способів вибору голосної літери є 5 способів вибору приголосної літери. Тому пару із голосної та приголосної літер можна вибрати 2·5=10 способів.

При розв’язуванні більш складних задач часто доводиться комбінувати правило суми і правило добутку.

Приклад 3.

Скільки чисел від 0 до 99 не містять у своєму записі цифру 5?

Розв’язання.

Спочатку порахуємо однозначні числа. Таких чисел може бути 8. А саме: 1, 2, 3, 4, 6, 7, 8, 9. Тепер порахуємо двозначні числа. Їх можна утворити, приписавши до будь-якого однозначного числа праворуч будь-яку із 9 можливих цифр (0, 1, 2, 3, 4, 6, 7, 8, 9). За правилом добутку таких двозначних чисел можна утворити 8·9=72. А разом однозначних та двозначних чисел, які задовольняють умову задачі, буде (за правилом суми) 72+8=90.

Часто один і той же об’єкт вибирають кілька разів. Тоді для отримання правильного результату потрібно відкинути повторні вибори.

Приклад 4.

Скількома способами із 28 кісток доміно можна обрати дві кістки так, що їх можна було прикласти одну до одної (тобто щоб деяка кількість очок була на обох кістках).

Розв’язання.

Спочатку оберемо одну кістку. Це можна зробити 28 способами. При цьому в 7 випадках обрана кістка виявиться дублем, тобто кісткою виду 0/0, 1/1, 2/2, 3/3, 4/4, 5/5, 6/6, а у 21 випадку – кісткою з різною кількістю очок (наприклад 0/2 або 3/5). У першому випадку другу кістку можна обрати 6 способами (наприклад, якщо на першому кроці була обрана кістка 1/1, то на другому кроці можна взяти одну із кісток 1/0, 1/2, 1/3, 1/4, 1/5, 1/6). У другому випадку другу кістку можна обрати 12 способами (для кістки 3/5 підійдуть як кістки 3/0, 3/1, 3/2, 3/3, 3/4, 3/6, так і 5/0, 5/1, 5/2, 5/4, 5/5, 5/6). За правилом добутку в першому випадку отримаємо 7·6=42 вибори, а в другому 21·12=252 вибори. Отже, за правилом суми отримуємо 42+252=294 способи вибору пари. У наведених міркуваннях враховувався порядок, у якому обирались кістки. Тому кожна пара була порахована двічі (наприклад, у першому випадку 1/1 та 1/6, а в другому – 1/6 і 1/1). Відповідно отриману кількість виборів потрібно поділити на 2. 294/2=147.

Задачі для самостійного розв’язання.

1. Скільки всього існує чотиризначних чисел?

2. Скільки тризначних чисел містять у своєму записі рівно одну цифру 3?

3. Скільки тризначних чисел містять у своєму записі хоча б одну цифру 3?

4. Учень виписав підряд всі тризначні числа. Скільки разів він написав цифру 3?

5. Скількома способами можна вказати на кубі дві сусідні грані?

6. Скільки існує різних прямокутників із цілими сторонами й периметром рівним 2014?

7. Скільки всього існує семизначних чисел, які складаються із 4 одиниць та 3 нулів?

8. Скільки всього існує семизначних чисел, цифри в запису яких розташовані в порядку зростання?

9. Скільки всього існує семизначних чисел, цифри в запису яких розташовані в порядку спадання?

10. На двох паралельних прямих розташовані точки (точки не співпадають): на одній – 3 точки, на другій – 6 точок. Скільки існує трикутників із вершинами в цих точках?

11. Скільки існує різних трикутників із цілими сторонами від 11 до 20?

12. Скількома способами можна набрати намисто із 7 червоних та 3 синіх бусинок?

13. Скількома способами можна набрати намисто із 7 червоних та 3 синіх бусинок так, щоб поруч не було синіх бусинок?